等风的鸟原创出品,转载须经同意并附带说明及地址。
逻辑回归应该是机器学习里入门级的算法了,但是越是简单的东西越是难以掌控的东西,因为你会觉得简单而忽视掉这个点,但恰恰这个点包含了机器学习的基本内容,学习的框架。
很多人学机器学习,人工智能可能就是为了更高的薪水,更好的就业前景,毕竟整个社会整个环境大家讲的都是这个,所以这个行业里的钱也最多。但是很多人只见其形却不懂得其内里的含义,我觉得机器学习学习的不仅仅是使用了哪个算法,而应该是一种思维,一种机器学习或者说人工智能这个行业发展的基础,发展的历程以及发展的未来。
言归正传,一句话就是,做机器学习不仅仅是做一个调参工程师,我们要想让机器学习人类首先我们要先学会让机器知道学习,那学习的基础就是数学。数学是人与机器交互最大的子集。
首先说一下逻辑回归,我的机器学习有两个路子,一个是吴恩达的机器学习视频,这个在网易公开课上就有,另一个就是《机器学习实战》,前者给我智慧,后者给我力量。开个玩笑,这两者其实就是理论和实践的代表,知行合一的体现。
首先说一下理论,吴恩达在视频中介绍逻辑回归的时候选用的是sigmoid函数,而sigmoid函数的另一个名称就是logistic函数,这也是逻辑回归(LogicRegression)的由来。而我什么选择sigmoid函数,我们需要先来看一下sigmoid函数到底长的什么样子:
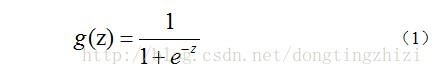
那么这就是sigmoid函数的表达式,下图是其函数图像
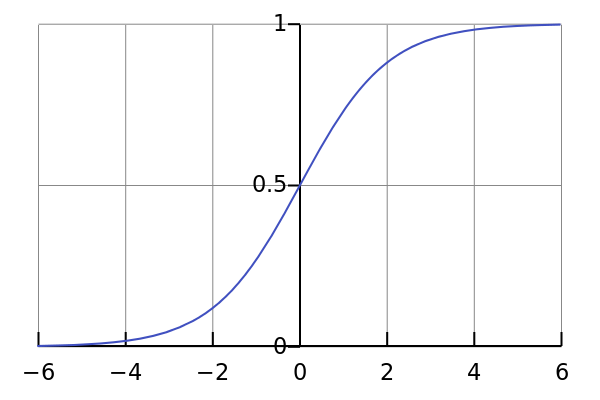
上图很明显的显示出了这个函数被选中的理由,天选之子出生自带的光环属性,这是一个Y取值范围为(0,1)的函数,而(0,1)也正是一个事件发生可能性的取值范围,同时其取值中心是0.5。这就是个很有趣的事情了,我在网上找到一个比较靠谱的解释:
为什么要选用sigmoid函数呢?为什么不选用其他函数,如probit函数?
其实,无论是sigmoid函数还是probit函数都是广义线性模型的连接函数(link function)中的一种。选用联接函数是因为,从统计学角度而言,普通线性回归模型是基于响应变量和误差项均服从正态分布的假设,且误差项具有零均值,同方差的特性。但是,例如分类任务(判断肿瘤是否为良性、判断邮件是否为垃圾邮件),其响应变量一般不服从于正态分布,其服从于二项分布,所以选用普通线性回归模型来拟合是不准确的,因为不符合假设,所以,我们需要选用广义线性模型来拟合数据,通过标准联接函数(canonical link or standard link function)来映射响应变量,如:正态分布对应于恒等式,泊松分布对应于自然对数函数,二项分布对应于logit函数(二项分布是特殊的泊松分布)。因此,说了这么多是想表达联接函数的选取除了必须适应于具体的研究案例,不用纠结于为什么现有的logistic回归会选用sigmoid函数,而不选用probit函数,虽然网上也有不少说法说明为什么选择sigmoid函数,例如“该函数有个漂亮的S型”,“在远离x=0的地方函数的值会很快接近0/1”,“函数在定义域内可微可导”,这些说法未免有些“马后炮”的感觉,哪个说法仔细分析都不能站住脚,我觉得选用sigmoid函数也就是因为该函数满足分类任务,用的人多了也就成了默认说法,这跟给物体取名字有点类似的感觉,都有些主观因素在其中。引自:https://blog.csdn.net/wolfblood_zzx/article/details/74453434?utm_source=copy
说完sigmoid函数,下面该是逻辑回归的公式推导了,这个个人感觉很重要,但是介于公式输入很繁琐,楼主在网上找到一个很靠谱的公式推导博文:
http://www.hanlongfei.com/机器学习/2015/08/05/mle/
就楼主搜索来说,这个是最舒服的了,还有一个就是CSDN上洞庭之子的推导也还是不错,这里尤其要注意的是,sigmoid函数求导之后的多项式的特殊性,即下文中第三行最后多项式的变换,有兴趣的写一下sigmoid函数的导数就可以了。
最后一行也就是《机器学习实战》中作者提到的有兴趣的同学可以推导一下的代码的来源。
#极大似然估计和梯度下降法明天更新吧。。。睡觉了
ok,继续未完成的内容。
首先说一下极大似然估计,这个在我考研时让我感到万分折磨的公式,现在回头想想,确实有着他的魅力,但是使用极大似然估计有一个前提,就是你要知道他的概率密度函数,这是一个很重要的问题,因为大多数情况下,我们不知掉所要预测的东西的概率密度函数,毕竟知道概率密度函数这就不是一个容易的事。所以对于逻辑回归来说,极大似然估计像是为他而生的一样,因为我们有逻辑回归的概率密度函数:sigmoid函数。具体的极大似然估计的求解方法,建议找一个考研班的视频,(建议张宇)这个很容易就可以理解,主要就是概率密度函数相乘,求得让这些已知样本可以发生的最大可能性的未知参数,因为相乘的就是1或者0的概率,也就是所拥有样本实现的可能性,所以这就是其数学依据。至于求解上文已经说明了,主要注意sigmiod函数求导所得的特殊性。
接着说一下梯度下降法,梯度下降法是用来求最优解(有时候是次优解,因为其容易陷入局部最优解中),而我们在极大似然估计中的求解正好需要梯度下降法来帮助我们求得我们想要的结果,或者说逼近一个最优解或者次优解。梯度下降法就是对多项式求导,沿着导数的方向是其减小最快的方向,这个要是不明白的话,建议还是看看考研高数,导数的含义。所以梯度下降法是我们求极小值的利器,对应的梯度上升法就是求极大值的了,这个没有什么好说的。当然我们为什么要求极小值,是因为我们选用的代价函数,也叫损失函数(通常是 预测值-真实值),我们肯定希望损失函数越小越好,毕竟损失函数越小代表我们越接近真实的情况,因为我们的预测值和真实值的差值最小了嘛。
因此最终我们就能得倒了我们梦寐以求的未知的参数了。
总结一下,其实整个算法就是一道求解数学题的过程,不过我们要自己出题自己选未知数,利用我们丰富的已知条件。当然,我们最后求得的很有可能是一个次优解,效果不是那么的理想,anyway,总比瞎猫碰死耗子的几率大不是。把每一个算法当作是求解一道数学题,在求解的过程中,我们可能会用到不同的方法或者多个方法去逼近未知数的真相,这也是对于同样的问题,为什么有这么多的算法,各种算法都有其优点和缺点,在面对具体的问题时,我们需要用不同的眼光去看待解决,经验可能会给我们一些便捷的方法,重要的是你要学着去把这道题解出来。
关于其中的具体推导公式,本文就不一步一步写下来了,因为文中已经给出了前辈的血汗,本文只是将其中的逻辑从头到尾讲清楚,并对其中的重点和难点进行了讲解,其实最主要的还是算法的逻辑,解题的思维。
希望能对大家的学习有帮助。期待下一节与你们再会。